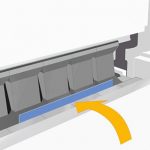
1. झुकाउने प्रक्रिया बुझ्दै: सरल तथ्यहरू
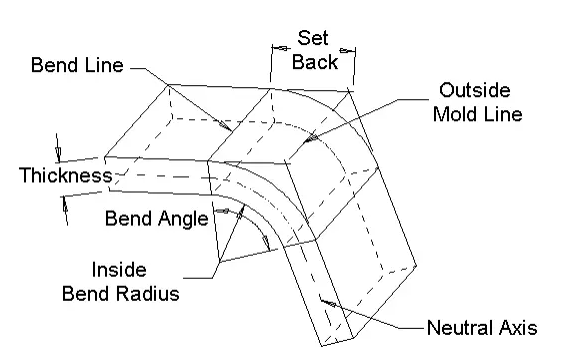
बेन्ड भत्ता = कोण * (T/ 180)*(रेडियस + K-फ्याक्टर *मोटाई) बेन्ड क्षतिपूर्ति = बेन्ड भत्ता-(2 * पछाडि सेट)
भित्री सेट ब्याक = ट्यान (कोण / 2) * त्रिज्या बाहिरी सेट ब्याक = ट्यान (कोण / 2) * (रेडियस + मोटाई)

1) झुकिएको भागमा प्राप्त त्रिज्याले हामीले त्यो भाग (मोड्नु अघि) काट्नु पर्ने लम्बाइलाई असर गर्छ।
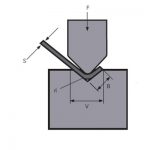
2) झुक्दा प्राप्त त्रिज्या हामीले काम गर्न रोजेको V ओपनिङमा 99% निर्भर गर्दछ।
भाग डिजाइन गर्नु अघि र खाली ठाउँहरू काट्न सुरु गर्नु अघि, हामीले प्रेस ब्रेकमा भागलाई मोड्नको लागि कुन V ओपनिङ प्रयोग गर्नेछौं भनेर ठ्याक्कै थाहा हुनुपर्छ।
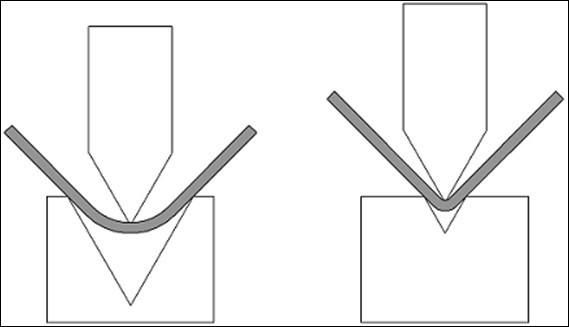
2. कसरी त्रिज्याले खाली ठाउँहरूलाई असर गर्छ
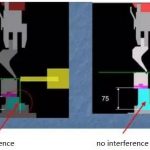
एउटा ठूलो त्रिज्याले हाम्रो भागको खुट्टालाई बाहिरी तर्फ "धकेल" दिनेछ, खाली भाग "धेरै लामो" काटिएको छ भन्ने छाप दिन्छ।
सानो त्रिज्यालाई एउटा खाली चाहिन्छ जुन त्रिज्या ठूलो भएको भन्दा "थोरै लामो" काट्नु पर्छ।
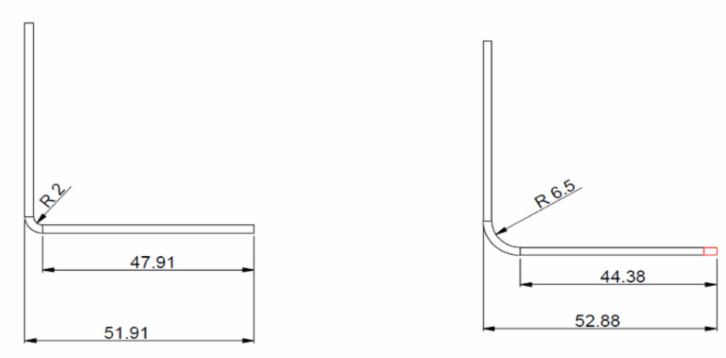
3. झुकाउने भत्ता
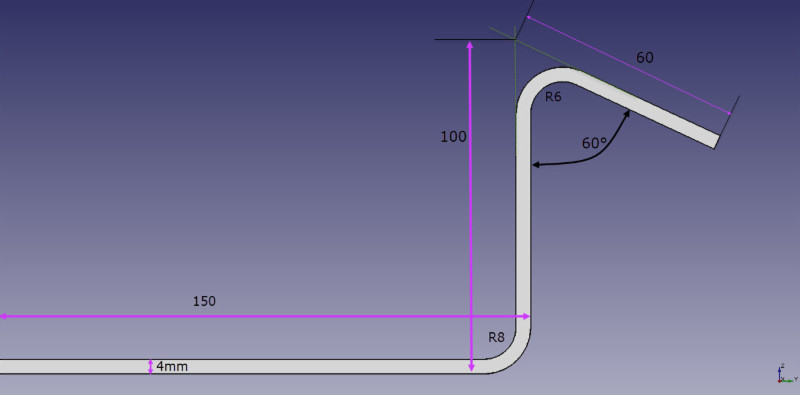
माथिको आंकडाको खुला खाली ठाउँहरू निम्नानुसार गणना गरिनेछ:
B = 150 + 100 + 60 + BA1 + BA2
BA1 र BA2 कसरी गणना गर्ने:
झुकाउने भत्ता गणना गर्दै
एक पटक समतल भएर ओभरल्याप भएपछि दुवै खुट्टाबाट घटाउनु पर्ने भाग, जसलाई हामी सामान्यतया "बेन्ड भत्ता" (वा समीकरणमा BA) भनेर चिन्छौं।
झुकाउने भत्ता सूत्र
90° सम्म झुकाउनको लागि BA सूत्र
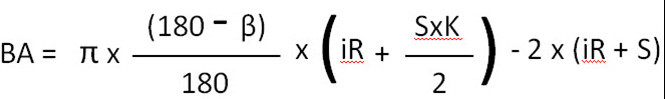
91° देखि 165° सम्म झुकाउनको लागि BA सूत्र
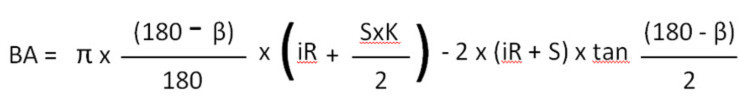
iR = आन्तरिक त्रिज्या
S = मोटाई
Β = कोण
Π = 3,14159265…
K = K कारक
K कारक
प्रेस ब्रेकमा झुक्दा पाना धातुको भित्री भाग संकुचित हुन्छ जबकि बाहिरी भाग विस्तारित हुन्छ।
यसको मतलब त्यहाँ पानाको एक भाग हो जहाँ फाइबरहरू न संकुचित वा विस्तारित छन्। हामी यस भागलाई "तटस्थ अक्ष" भन्छौं।
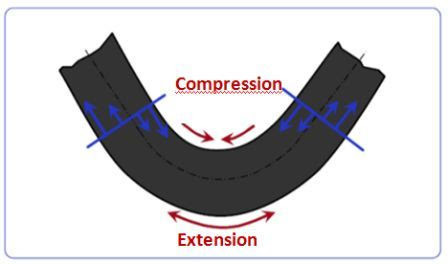
बेन्डको भित्री भागबाट तटस्थ अक्षसम्मको दूरीलाई हामीले K कारक भनिन्छ।
यो मूल्य हामीले खरिद गरेको सामग्रीसँग आउँछ र यसलाई परिवर्तन गर्न सकिँदैन।
यो मान अंशहरूमा व्यक्त गरिएको छ। K कारक जति सानो हुन्छ, तटस्थ अक्ष पानाको भित्री त्रिज्याको नजिक हुनेछ।
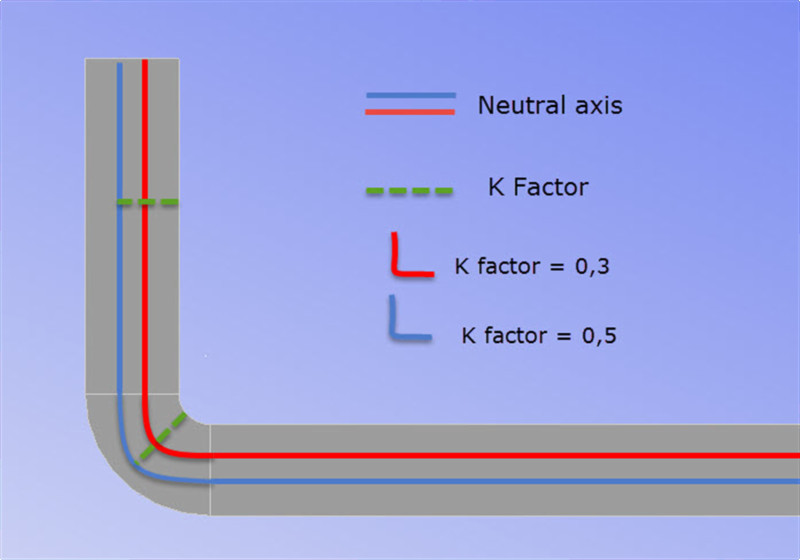
K कारक = ठीक ट्यूनिंग
K कारकले हाम्रो अनफोल्ड गरिएको खालीलाई असर गर्छ। भागको त्रिज्या जत्तिकै होइन, तर हामी यसलाई खाली ठाउँहरूको लागि राम्रो ट्युनिङ गणनाको रूपमा सोच्न सक्छौं।
K कारक जति सानो हुन्छ, अधिक सामग्री विस्तारित हुन्छ र त्यसैले "बाहर धकेलिन्छ"…। जसको अर्थ हाम्रो खुट्टा "ठूलो" हुनेछ।
K कारक अनुमान गर्दै
धेरै जसो समय हामीले हाम्रो खाली गणनाहरू राम्रोसँग ट्युन गर्दा K कारकलाई अनुमान गर्न र समायोजन गर्न सक्छौं।
हामीले गर्न आवश्यक छ केहि परीक्षणहरू (चयन गरिएको V ओपनिङमा) र भागको त्रिज्या नाप्नुहोस्।
यदि तपाइँले थप सटीक K कारक निर्धारण गर्न आवश्यक छ भने, तल तपाइँको झुण्डको लागि सही K कारक निर्धारण गर्नको लागि गणना छ।

K कारक: एक सूत्र
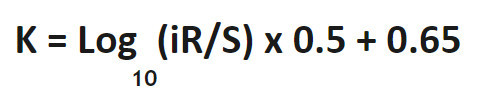
उदाहरण समाधान:
B = 150 + 100 + 60 + BA1 + BA2
K कारक अनुमान
B1: R/S=2 => K=0,8
B2: R/S=1,5 => K=0,8
दुबै झुण्डहरू ९०° वा कम छन्:
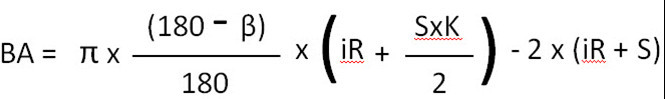
भन्नाले:
B1 = 3.14 x 0.66 x (6 + ((4×0.8)/2) - 2 x 10
B1 = -4.25
B2 = 3.14 x 0.5 x (8 + ((4×0.8)/2) – 2 x 12
B2 = -8.93
त्यसैले:
B = 150 + 100 + 60 + (-4.25) + (-8.93)
B = 296.8 मिमी